How do I Calculate the Area of a Circle?

The Area of a Circle

There are a few things we need to know when calculating the area of a circle, and it’s always good to start with the basics. A circle is a 2D shape — like any other 2D shape, its area is the amount of space it covers. The bigger the circle, the bigger the area.

Unlike polygons such as rectangles or parallelograms, we can’t multiply together the lengths of the sides to find the area. Instead, we use the distance from the edge of the circle to the centre.

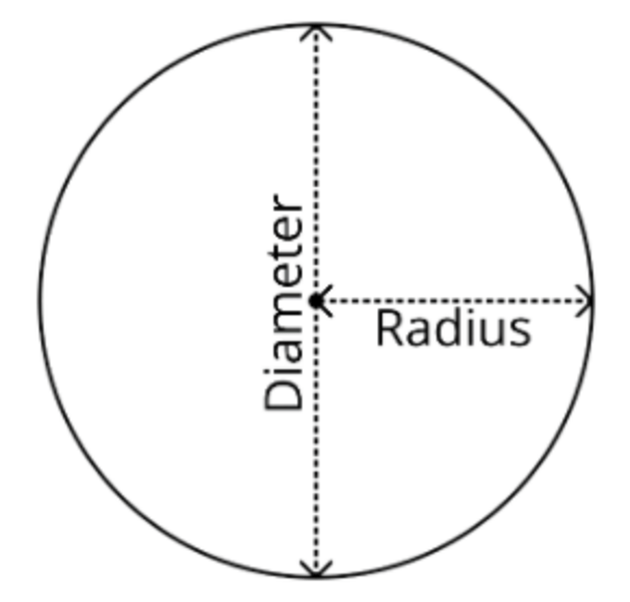
There are two measurements you need to be aware of here:

• The radius is the distance from the edge of the circle to the centre.
• The diameter is the distance from one side of the circle to the other, through the centre of the circle.

The diameter is twice the length of the radius, the radius is half the length of the diameter. Keep reading to find out how to work out the area of a circle using the diameter.

How to Calculate the Area

If we split a circle into sectors and then rearrange them, we get a shape that is approximately a parallelogram.

The vertical height of the parallelogram is the radius of the circle, r, but how do we calculate the length of the base of the parallelogram, b?

The length of the base is half the circumference of the circle. As we calculate the circumference using the formula C = 2πr,

b = 1/2 × 2πr

= πr

Therefore, we can calculate the area of the parallelogram and thus the area of a circle.

Area of a circle = π × r × r

= πr²

A reminder that π is a Greek letter, spelt pi and pronounced like pie. Pi is a constant, which means it never changes. It is also irrational, which means it never ends and never repeats. The first 20 digits are:

• 3.14159265358979323846…

If you’re using π to find the area (or circumference) of a circle, you can either use the π button on your calculator or round it to 3.14.

Example 1 — Find the area of a circle using the radius of 5cm. Give your answer correct to 1 decimal place.

Area = π × radius × radius

We know the radius, so put it into the formula above:

• Area = π × radius × radius
• Area = π × 5 × 5
• Area = 78.5cm² (to 1d.p.)

Make sure you give the correct units. Like any other area, the area of a circle is given in square units. That may be cm², m², mm² or km², among others.

Let’s go through another example.

Example 2 — Find the area of a circle using the radius of 17cm. Give your answer correct to 1 decimal place.

Area = π × radius × radius

We know the radius, so put it into the formula above:

• Area = π × radius × radius
• Area = π × 17 × 17
• Area = 907.9cm² (to 1d.p.)

How to work out the area of a circle using the diameter

In maths, you will not always be given the radius of a circle. However, it is still possible to find the area. Here are the steps you must take to work out the area of a circle using the diameter:

Step 1: Find the radius

The radius is equal to half of the diameter. So, in order to find the radius, we must divide the diameter by 2:

radius = diameter ÷ 2

Step 2: Use formula using the radius

Now, that we know the radius, we can use the same formula for the area as before.

Area = π × radius × radius

We are multiplying r by itself in this equation, which means that we are squaring it. So, the formula can be simplified to this:

• A= π × r²

Finally, because this is an algebraic formula, we can remove the × sign:

• A= πr²

Let’s put this into practice with an example.

Example 1 — Find the area of a circle using the diameter of 14m. Give your answer correct to 1 decimal place.

Be careful! In this question, we have been given the diameter, but we need the radius to find the area.

The radius is half the diameter:

• radius = diameter ÷ 2
• radius = 14 ÷ 2
• radius = 7m

We can now find the area as before:

• Area = π × radius × radius
• Area = π × 7 × 7
• Area = 153.9m²

Here’s another example of how to find the area of a circle using the diameter:

Example 2 — Find the area of a circle using the diameter of 32m. Give your answer correct to 1 decimal place.

The radius is half the diameter, so:

• radius = diameter ÷ 2
• radius = 32 ÷ 2
• radius = 16m

Now, we can find the area using the original formula:

• Area = π × radius × radius
• Area = π × 16 × 16
• Area = 804.2m²

How to work out the area of a circle using the circumference

In some cases, you will find that the radius and the diameter of a circle are unknown. Fear not, you can still calculate the area of a circle using the circumference. The circumference is the total distance around the circle. The formula for finding the circumference of a circle is:

C = 2πr

We can use this to find the radius of the circle and then once we have this, we can find the area of the circle.

Let’s show you how to do this with an example.

Example 1 — Find the area of a circle with a circumference of 3m. Give your answer correct to 1 decimal place.

First, let’s use the formula for the circumference of a circle and substitute our value for the circumference into it.

C = 2πr

3 = 2πr

r = 3/2π cm

Now we have the radius of the circle, we can use it to find the area as we have before.

• Area = π × (3/2π)²

Area = 0.7m² (1d.p.)

Resources to Support Your Teaching

We have created a wide range of engaging and effective resources to assist your maths teaching. These resources include challenging worksheets, informative PowerPoints, fun games, and activity sheets. Everything at Twinkl is made by teachers, for teachers, so you can be sure you are getting the highest quality resources. What’s more, they are all really easy to download and use, helping you cut down your preparation time to a minimum.

If you're looking for resources for kiddos in EYFS, we have loads of lovely materials to introduce them to the shapes on our Circles and Triangles Category Page. We also have this fun I Spy Circles Activity, perfect to introduce younger tots to the concept of shape!

If you're teaching children in KS1, some of our favourite KS1 resources for finding the area include:

• Introduction to Area PowerPoint: This PowerPoint is the ideal introductory activity for kids who are just getting started with finding the area. It is perfect for assisting your teaching of how to work out the area of a circle using the diameter, radius, and more. This PowerPoint presents information in a colourful, engaging format in a manner that is easy to understand.

Follow up this PowerPoint with these handy worksheets:

• Calculate the Area Worksheets: These worksheets are ideal for supplementing your maths lessons and require no effort or preparation to use. Kids will be presented with a variety of regular shapes in these differentiated worksheets, which they must calculate the area of. There are four area worksheets included in this pack. Two of these worksheets require students to count squares to work out the area, while the other 2 require them to use a ruler and the geometric formulas that they have learned. Use these worksheets either in class or as a homework activity.
• Create and Find the Area Differentiated Worksheets: Get kids to consolidate their knowledge of finding the area with these differentiated worksheets. This resource is ideal for mixed-ability classrooms, as they are carefully differentiated. There are three worksheets included in this pack, for lower ability, middle ability, and higher ability students. To complete each activity, kids must first create a shape using cubes and then find the area of it. Answer sheets are included with each worksheet, so marking will be a breeze!
• Iceberg Triangle Area Differentiated Worksheets: These iceberg differentiated worksheets are a super fun way of getting kids to practice finding the area of various triangles. There are three levels of difficulty for the iceberg worksheet included in this pack, so it’s easy to use in a mixed-ability classroom.

If your kids are older, check out these lovely KS2 resources for finding the area:

• Calculate Area Interactive PowerPoint: This PowerPoint is a fantastic tool for getting your students to solidify their understanding of finding the area. There are 33 different maths problems in this resource, each of which varies in difficulty.

Follow up this PowerPoint with these handy worksheets:

• Calculating the Area of Compound Shapes Worksheet Pack
• Measuring Area of Chocolate Boxes Worksheet
• Compound Area Differentiated Worksheets